Medians and Altitudes of a Triangle

Construct the $△ABC$ such that $AB=6 \mathrm{cm}, BC=7 \mathrm{cm}$ and $AC=5 \mathrm{cm}$. Locate its centroid.

Find the co-ordinates of the foot of the perpendicular drawn from the point $P(1,2)$ the line $3x-4y-16=0$.

In $\Delta DEF, DN, EO, FM$ are medians and point $P$ is the centroid. Find the following.

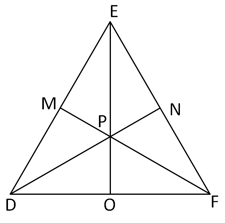
If $PD=10, PF=12, PE=8$, then find $PN,PM,PO$

The coordinates of the vertices of a triangle are$(1,2),(3,3),(1,1).$ Find the coordinates of its centroid.

Name the orthocentre of $△PQR$.

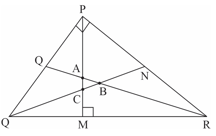
If $G$ is the centroid of a $△ABC$ and $P$ is any other point in the plane, then $P{A}^2+P{B}^2+P{C}^2$ is equal to

In $△ABC,$ the median $AD, BE$ and $CF$ passes through the point $G$. If $AD=7.5 \mathrm{cm},$ then find $GD$ (in $\mathrm{cm}$) (correct up to one decimal place)

In $△ABC,$ the median $AD, BE$ and $CF$ passes through the point $G$. If $GF=4 \mathrm{cm}$ then, find $GC$ (in $\mathrm{cm}$).

The perpendicular from the vertex of a triangle to the side is called _____ of the triangle.

In a triangle $ABC, H$ is the orthocentre. $X, Y$ and $Z$ are midpoints of $AH, BH$ and $CH$ respectively prove that orthocentre of $△XYZ$ is $H$.

In a $△ABC, P$ is the orthocentre. Prove that orthocentre of $△PBC$ is $A$.

The triangle whose ortho centre is its vertex point is called.

If two medians of a triangle are equal, then the triangle is

Gravitation centre of a triangle

In $△ABC$, medians $AD, BE$ and $CF$ intersect each other at$G$. Prove that $AD+BE>\frac{3}{2}AB$.

In the $△\mathrm{ABC}$ medians $\mathrm{AD}, \mathrm{BE}$ and $\mathrm{CF}$ intersect each other at $\mathrm{G}$. If $\mathrm{AG}=6 \mathrm{cm}, \mathrm{BE}=9 \mathrm{cm}$, and $\mathrm{GF}=4.5 \mathrm{cm}$. Find the length of $\mathrm{GD},\mathrm{BG}$ and $\mathrm{CF}$.

In triangle $PQR$, $PS$ is a median and $QS=3.5 \mathrm{cm}$ and $QR=k \mathrm{cm}$, find the value of $k$.

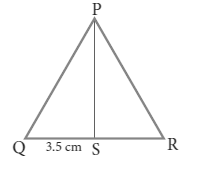
In the triangle $ABC$,

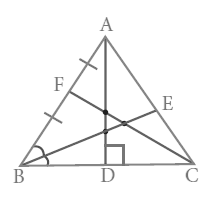
The median is _____$(CF, BE, AD)$ .

Where does the orthocentre lie in the case of a right angled triangle?

Where does the orthocentre lie in the case of an obtuse-angled triangle?